All laws of thermodynamics are nothing but hypotheses built on scientific observations of the processes that occur in nature. It would not be naive to state that all these laws are the expression of natural laws. The first law of thermodynamics, in simple words, is the specific form of the conservation of energy principle, which states that:
“Energy can neither be created nor destroyed. It converts from one form to another.”
So, how is the first law of thermodynamics related to the energy principle?
For a thermodynamically closed system (control mass) undergoing cyclic processes, the first law states that:
The change in the total energy of the system is zero (energy conservation principle); as a result, the net heat supplied to such a system is equal to the net work done by the system on its surroundings.
The first law of thermodynamics cannot be fully understood without considering key mathematical expressions. For that, one needs to write an energy equation for a control mass and then draw from it the equation of the first law of thermodynamics.
The Energy Equation For First Law of Thermodynamics
It is important to note that the total energy (E) associated with a substance is composed of its internal energy (U), kinetic energy (KE), and potential energy (PE). Internal energy is associated with the microscopic forms of energy at the molecular level, such as linear/rotational kinetic energy, nuclear energy, electron spin, etc. Thus:
E_{total}=U+KE+PEOr, in terms of specific energy (which is defined as the energy per unit mass, e=E/m), one can write the above equation as:
E\;=\;me
E_{total}=\;m(u\;+\;\;ke+pe)Where u, ke, and pe stand respectively for specific internal, kinetic, and potential energy. Elaborating the above equation gives rise to the following expression:
E_{total}\;=\;m(u\;+\;\frac{V^2}2\;+\;gZ)Kinetic energy and potential energy are concerned with the physical state and location of the mass, and both are interconvertible to each other and are generally labeled as mechanical energy. Whereas internal energy is associated with the thermodynamic state of the mass, it is called thermal energy.
Thus, one can write the total energy difference of a control volume when it undergoes from state 1 to state 2 in differential form as follows:
dE_{cv}\;=\;dU\;+\;d(KE)\;+\;d(PE)Integrating the above equation on each side separately thus gives rise to:
\int dE_{cv}=E\left(t_2\right)-E\left(t_1\right)=E_2-E_1\int\left[dU\;+\;d\left(KE\right)\;+\;d(PE)\right]\;=\;\left(U_2\;-\;U_1\right)\;+\frac12m\left(V_2^2\;-\;V_1^2\right)\;+\;mg\left(Z_2\;-\;Z_1\right)
Combining the two gives rise to:
E_2\;-\;E_1\;=\left(U_2\;-\;U_1\right)\;+\;\frac12m\left(V_2^2\;-\;V_1^2\right)\;+\;mg\left(Z_2-Z_1\right)
The above equation explains the energy change of a system in terms of its internal, kinetic, and potential energies. So, for the stationary system in which the change in kinetic and potential energy is zero, the total energy change of the system is at the level of its internal energy.
In order to write the energy balance equation, consider a control volume with fixed mass under thermodynamic study as stated above. Its total energy (Ecv) in terms of the instantaneous rate of change of energy of the control volume or other words, at a specific point in time is thus:
\frac{dE_{cv}}{dt}\;=\overset.E_{cv}\;=\frac{dQ}{dt}\;-\;\frac{dW}{dt}\frac{dE_{cv}}{dt}\;=\overset.E=\;\overset.Q-\overset.WIt is shown schematically below:
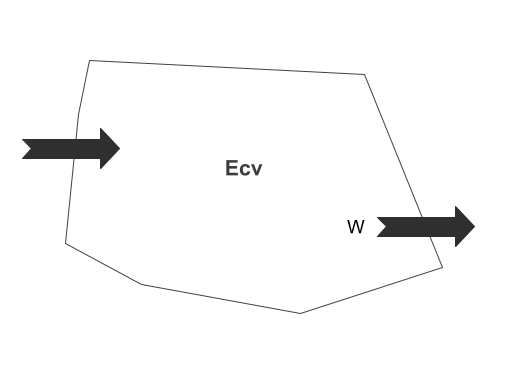
In engineering practices, one is more concerned with the system in the process from initial to final state than at a specific point in time. Therefore, we multiply the equation 3 by dt and then integrate it from the initial state (t1) to the final state (t2):
dE_{cv}\;=\;\left(\overset.Q\;-\;\overset.W\right)dtIntegrating the left side separately,
\int dE_{cv}\;=\;E\left(t_2\right)\;-\;E\left(t_1\right)\;=\;E_2\;-\;E_1Integrating the right side separately,
\int\left[Q\;-\;W\right]\operatorname dt=\;\int_{Path}\delta Q\;-\;\int_{Path}\;\delta W\;=\;Q_{1-2}\;-\;W_{1\;-\;2}Combining the two sides of equation 04 gives:
E_2\;-\;E_1\;=\;Q_{1-2}\;-\;W_{1-2}As the change in the total energy of the control volume is equal to the net heat supplied and net work performed, comparing the two equations 01 and 05 gives rise to the final energy balance expression:
Q_{1-2}-W_{1-2}\;=\;\left(U_2\;-\;U_1\right)\;+\;\frac12m\left(V_2^2\;-\;V_1^2\right)\;+mg\left(Z_2-Z_1\right)In engineering practices, we encounter cyclic processes; that is, the system at the end of the process reaches its initial state, which means that the final energy is equal to the initial energy or the change in energy is zero. In this specific case, the energy equation takes the following form:
Q_{1-2}-W_{1-2}\;=\;0Or in integral form:
\oint\delta Q-\oint\delta W=0
Where;
𝛅Q is the cyclic integral of the heat transfer during the process, and 𝛅W is the cyclic integral of the work showing the net work output performed by the system on its surroundings.
If we rewrite the above equation,
\oint\delta Q=\oint\delta W
The above equation is the expression of the first law of thermodynamics:
When a system (say control volume) undergoes a thermodynamic cycle, the net heat supplied to the system during the cycle is equal to the net work done by the system on its surroundings.
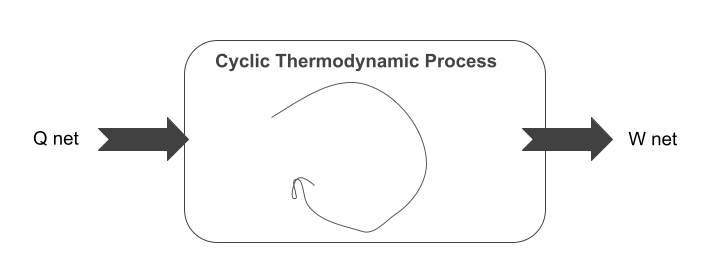
It is illustrated schematically above.
The final integral expression is chiefly used for the thermodynamic cycles actualized in the case of steam engines and steam turbines, power plants, and so forth. However, with opposite sign conventions for heat transfers and net work done, one can state the same law for heat pumps and refrigerators as well.
I am the author of Mechanical Mentor. Graduated in mechanical engineering from University of Engineering and Technology (UET), I currently hold a senior position in one of the largest manufacturers of home appliances in the country: Pak Elektron Limited (PEL).
