Thermodynamics is the science of energy, or in simple words, it is the branch of scientific discourse that is concerned with the all-encompassing aspects of energy, its conversion or transformation.
Its name has its roots in the Greek language with the words therme (heat) and dynamis (power) which, when read collectively, show the key interest of the people of Ancient Greece in the conversion of heat into power, which constitutes the basis of applied thermodynamics.
Now, what is applied thermodynamics? It studies the interrelationship of heat, work, and the different properties of a system (which shall be described shortly), or it is focused on the means that can be utilized to convert the form of energy, that is, to change energy from its one mode to another, or more simply from heat (such as receivable from fossil fuels buried beneath the earth for centuries) to useful (mechanical) work.
Energy: Heat and Work
In the whole corpus of thermodynamics, energy is treated to have two forms: heat and work.
Heat
Heat is that form of energy that transfers from one reference point to another due to temperature differences.
It is always a transitory form of energy, which means that it is observable only during its transfer. It is the intrinsic energy of a body that it contains, not heat, which is the function of temperature.
Work
Likewise, work is that form of energy that is mobilized when a closed system under the sway of a certain force moves or is moved by its surroundings. In either case, work is performed.
It is also not containable in a body like heat. It is the energy in motion whose sole purpose must be to serve humanity and humanitarian causes. It should always be anthropocentric.
System, Surrounding and Boundary
A definite quantity of matter under scientific study is called the system. Anything outside it constitutes its surroundings, whereas a real or an imaginary surface separating the two is known to have constituted the boundary of the system, as illustrated below.
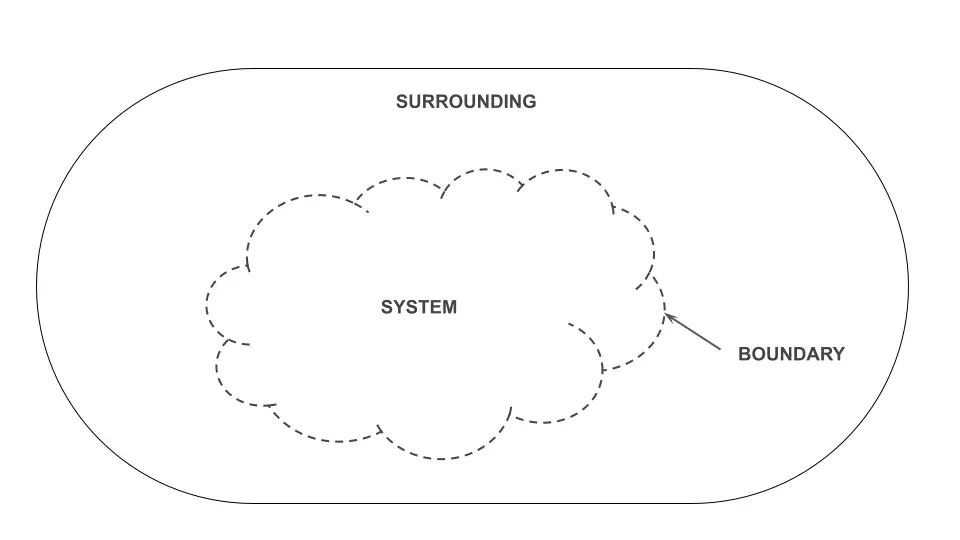
Interestingly, what if someone asks about the boundary and surroundings when space is to be studied as a system?
One must reply with tranquillity that only an arbitrary region of space under study constitutes a system, which means, say, any celestial body or object because space as a whole cannot be chosen as a (closed) system since it is indefinite.
Thus, an imaginary surface would be demarcated and called a boundary, and anything beyond that boundary should be called surrounding.
Open, Closed and Isolated System
Closed System
A closed system is one with its mass fixed; this means that a certain quantity of matter enclosed within cannot cross its boundary and enter into the surroundings. However, it does not prevent the exchange of energy into and from the system.
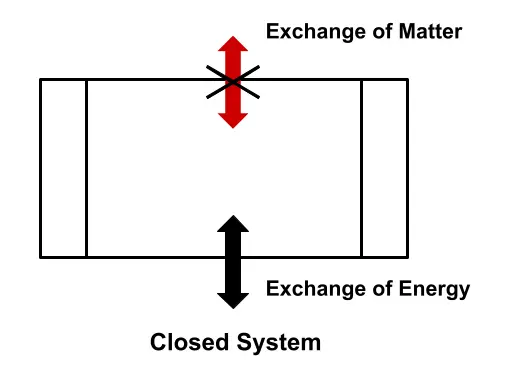
In short, in the closed thermodynamic system, which is also called a control mass, a certain quantity of mass contained cannot cross the boundary, but the energy in the form of heat and work definitely can.
For example, the gas contained in a piston-cylinder arrangement such that it may not escape through the boundaries. In this example, the boundary (piston head) is flexible as it moves either inwardly or outwardly, thus changing the volume inside the cylinder but the quantity of gas enclosed.
Other useful examples of a closed system include water contained in a sealed thermos flask, the gas stored in a closed pressure vessel, the earth’s atmosphere (in view of some scientists), and so forth.
Open System
An open system, which is also called a control volume, is one through which there is an exchange of mass as well as energy. Its boundary is called a control surface.
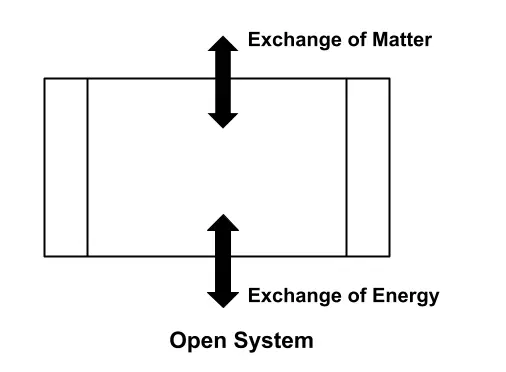
Its classic examples include fluids through a turbine, compressor, and nozzle, through which both mass and energy flow are possible. In engineering practices, they are control volumes that are more frequently analyzed than open systems.
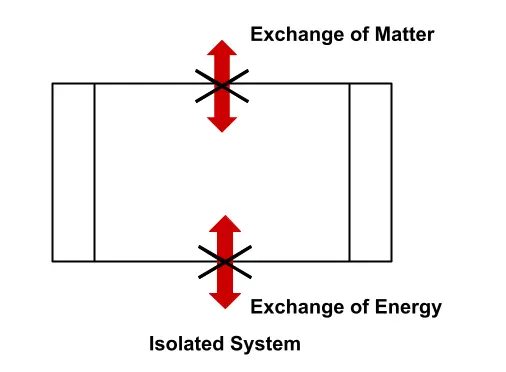
Isolated System
A system through which there is neither energy nor mass flow is possible is called an isolated system. A class of cosmologists argues that our whole universe can be treated as a closed system.
Properties of the System
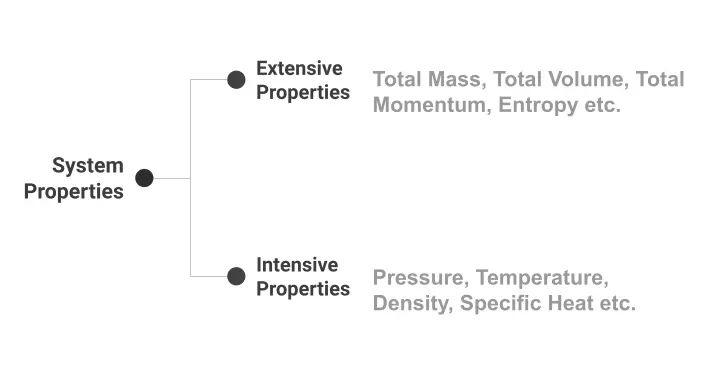
Intensive Properties
These are the properties of a system that do not depend on mass; that is, they are those properties which, for instance, by halving or doubling the mass of a gas enclosed in a chamber, do not change.
But what are these properties which remain unaffected when the mass of the system is varied? They include, for example, pressure, temperature, density, specific heat, molar mass, refractive index, and so on.
Extensive Properties
On the contrary, extensive properties depend on mass. That is, when the mass of a given system is varied, the value of extensive properties concomitantly changes.
These properties include total mass, total volume, total momentum, electric charge, entropy, enthalpy, and so on.
For understanding, one can say that the total electric charge of a system depends on the cumulative charge-particles present in the system, that is, the quantity of matter that are charged particles that carry the electric charge.
So, the value of the electric charge of a system proportionally varies once one changes the quantity of charged particles under study in the system.
One would fairly wonder when it comes to answering a rather tricky question: Is matter itself intensive or extensive property? Its answer is very obvious. Very briefly, mass is an extensive property because it depends upon the matter of a given scientific object under thermodynamic analysis.
Or, one can say, mass is only such an extensive property of a system which is solely the function of its own, only because it is subject to the matter of mass which makes any extensive property extensive.
Isothermal, Isobaric, Isochoric Process
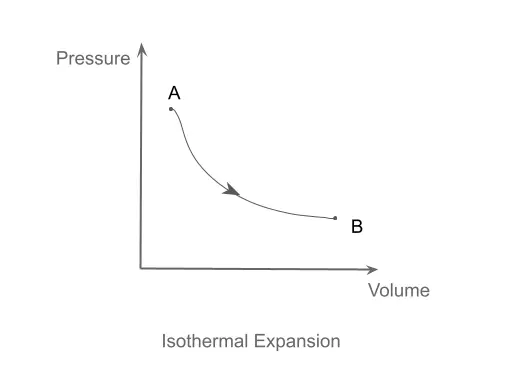
Isothermal Process
An isothermal process is one in which the temperature of the system remains constant. It is worthwhile to mention that a truly isothermal process is difficult to achieve due to heat losses and heat gains during the process.
A naive example of an isothermal process would be an ideal gas enclosed in a piston-cylinder arrangement. When heat is to be provided to such a system, in order to keep the temperature constant, the gas must expand to perform some work. This process is shown graphically in the PV diagram below.
Isobaric Process
In the isobaric process, the pressure of the system remains constant. Common examples of isobaric processes are those events that are performed at atmospheric pressure. It is shown graphically in the PV diagram below.
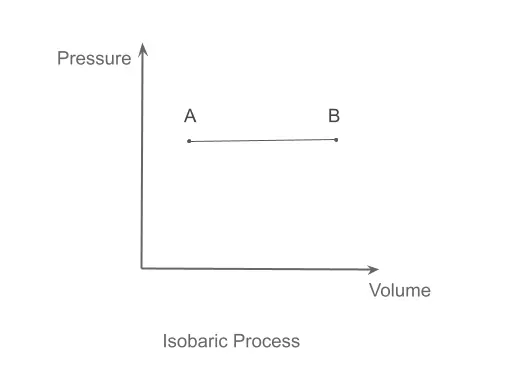
For example, a water container on an active stove with no lid on it would be a constant pressure process, which means, say, in the course of heating by the stove. However, the temperature of the water would increase, and the pressure inside would remain constantly atmospheric unless the top of the container or pot were covered with a lid.
Isochoric Process
During these processes, the specific volume of the system remains constant. (Specific volume is the total volume divided by the mass of the system; it shows the volume in cubic meters occupied by a 1-kilogram mass of the system.) It is shown graphically in the PV diagram below.
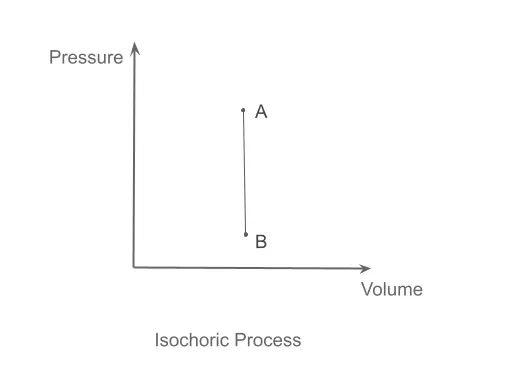
Achieving an isochoric process is a bit challenging because, during heating, thermal expansion takes place, thereby altering the specific volume of the work under study.
It is rather careful to put that no process is fully isothermal, isobaric, or isochoric. Instead, their consideration serves only theoretical purposes in the form of rational as well as quasi-natural assumptions, which are taken during analysis to study the process comfortably.
For example, in the study of an ideal Otto or diesel cycle, different processes are assumed to be isobaric and isochoric, which certainly are not in the practical engineering situation.
Laws of Thermodynamics
Thermodynamics has its laws, which can be understood as the natural hypotheses built upon the human perception of the world we inhabit. These laws are famously called the First and Second laws of thermodynamics. However, there are also the third law and Zeroth law of thermodynamics as well.
First Law of Thermodynamics
It is the scientific double of the law of conservation of energy; that is, energy can neither be created nor destroyed; however, it does change its form.
It asserts that energy is inevitably a thermodynamic property, which means that it is transformative. Its two modalities (forms) are heat and work. Any system that is under thermodynamic studies confirms the reality of the energy principle, which is the energy balance.
Again, in simple words, one can note that the first law of thermodynamics is nothing but the thermodynamic twist given to the principle of the conservation of energy in straightforward reference to thermal energy, which is heat, and mechanical energy, which is work.
More specifically, in the context of applied thermodynamics, according to the first law of thermodynamics, during a complete thermodynamic cycle, the intrinsic energy of the system at the beginning and the end remains the same.
Mathematically, one can write that the sum of net heat supplied and net work done is zero.
Second Law of Thermodynamics
The first law of thermodynamics gives a quantitative explanation of energy. The character of energy in the form of its quality is well explained by the second law of thermodynamics, which owes multiple statements in terms of entropy, irreversibility of a process, and heat flow.
- In terms of entropy, which is the measure of the disorder of a system, the second law states that the energy always flows in the direction of increasing entropy. That is, with time, energy flows in such a fashion that the randomness or the collective disorder of the system furthers.
- From the perspective of irreversibility, the second law asserts that certain natural processes are irreversible. For example, a hot cup of coffee placed inside a cold room would cool off spontaneously as a result of its heat loss to its surroundings (in accordance with the first law of thermodynamics). However, this process cannot be reversed until externally mediated, that is, the transfer of energy from the air back to the teacup.
- Finally, in the language of heat flow, the second law states that the heat flow is always in the direction from a high-temperature zone to that of a low. In this vein, the Kelvin-Planck statement, which says that it is impossible to construct a device that receives heat from a single source and gives a net amount of work, is very pertinent to include.
All these definitions of the second law of thermodynamics pointedly emphasize that in the natural course, the heat flow is always in the direction where there is a potential for increased entropy.
In the example of an ice cube placed in a hot room, energy will be lost by the ice cube and subsequently regained by the surrounding air so that the net entropy of ice plus environment may increase.
According to the second law, in the case of a heat engine, the working fluid can’t receive heat from a heating source such as a boiler and give net output by expanding fully into a steam turbine without losing some heat to the sink in order to keep the thermodynamic cycle going on.
It is not because there are really some frictions out there, but it is because there are certain advanced and complex mathematical models that can account for it.
All thermodynamic processes obey both the first and second laws of thermodynamics.
Third Law of Thermodynamics
It states that when the temperature of a pure crystalline substance drops to zero (absolute temperature, which is 0K or -273C), its entropy drops to zero. In simple words, the entropy of a substance at 0K is minimum.
The utility of the third law rests in the determination of reference point for defining absolute zero, of calculating the absolute entropy of a substance at a given specific temperature, in the study of phase transitions at lower temperatures, cryogenics, and so forth.
In short, the third law of thermodynamics is an important law that is concerned with the entropy of a system at lower temperatures, thereby rendering possible the calculation of absolute entropy at a given temperature.
It has vast applications in quantum mechanics in which it is used to investigate the quantum ground status of the systems and their behavior at considerably lower energy levels at 0K because, at this level, classical thermodynamics fails to study the quantum state of particles which is only concerned with the system at higher temperatures and elevated energy levels.
Zeroth Law of Thermodynamics
It states that if two bodies each are in thermal equilibrium with the third body, then these two bodies are also in thermal equilibrium with each other.
The obvious implication one can draw from this is that the three bodies are at the same temperature. This law finds its significance in defining temperature scales and comparing them with each other.
Entropy
It is the most important yet highly controversial concept in thermodynamics and university physics. Its name was first used by the scientist Clausius, who defined it as:
dS=\frac{dQ}THere, ‘d’ shows a very small quantity of q denotes heat, and T stands for absolute temperature.
In the simplest of words, it refers to descriptors such as disorder, chaos, spreading, freedom, or missing information at the molecular level of a system. For an isolated system, it remains constant or tends to increase; however, in a spontaneous process, it always increases.
Scientist Boltzmann claimed that when a system, initially present in its equilibrium state, is left to itself (or at its disposal), it moves in its natural course to a more disordered, probabilistic state. That’s why he called the second law of thermodynamics a probabilistic law with which the concept of entropy is fully linked.
Moreover, in advanced literature, entropy is treated as a mysterious term. Scientists or engineers use this term frequently without knowing its comprehensive meaning at all. It cannot be accounted for their intellectual ignorance or academic naivety.
Rather, it owes much to the mysterious character of the term entropy, as there is a class in the scientific community that asserts that its clear understanding can never be achieved.
Actually, each descriptor (such as disorder, chaos, missing information as mentioned above) is (mis)taken to deliver meaning for entropy: few scientists measure disorder in order to determine entropy or change in entropy. In contrast, others emphasized missing information or chaos to demystify the understanding of entropy.
Whatever it is, due to the brevity of space, we shall limit our understanding up to its simple development as a concept, yet believing its actual status in the scientific or scholarly community is pretty vague.
Steady and Unsteady Flow
Steady Flow
As the name implies, it is a fluid flow (working fluid) during which the fluid properties (say, pressure, volume, and total energy content) do not change with time; that is, they remain the same.
In engineering (fluid dynamics) theory, this kind of flow is taken as an ideal flow in control volumes because it is represented in approximations with the devices continuously in operation, such as water/steam turbines, pumps, compressors, heat exchangers and boilers with the exception of, for example, IC engines and heat pumps which are based on the cyclic process during which fluid properties do change with time albeit periodically.
The process which involves steady flow is called the steady flow process. A simple example of a steady flow process is the flow of cascading water falling on a hydro-turbine operating uninterruptedly.
Though the properties of the fluid may vary from point to point in the flow stream, they do remain the same, ideally speaking.
Unsteady Flow
It is also called a transient flow. It is a fluid flow during which the fluid properties do not remain the same, which means that they change over a while.
For example, the flood wave can be studied as an unsteady flow of water stream. Another crude example includes the flow of water through a tap when it has just been opened due to the unsteady flow rate of water.
One more example includes unsteady combustion in the internal combustion engine during fuel ignition.
Reversible and Irreversible Processes
Reversible Process
It is a process that can be reversed thermodynamically without leaving any trace in the surroundings in which the process occurs. In simple words, these are the processes that occur without the loss of heat. They are, in fact, ideal processes.
For example, a process carried out in a well-insulated system in which there is no cross of heat can be approximated as a reversible (adiabatic) process.
Another example includes an isothermal compression or expansion of an ideal gas in a piston-cylinder arrangement in which there is a continuous exchange of heat between air and its surroundings in order to keep the temperature unchanged.
Irreversible Process
It is a process that cannot be reversed thermodynamically as it does cause a (thermal) change in the surroundings in which the process occurs.
Actually, during their execution, the entropy of the system and the surroundings increases, which cannot be reversed, thus rendering the process irreversible.
In practical situations, its examples abound. For instance, the transfer of heat between two bodies is kept at a finite temperature difference: during the heat transfer process from the hotter to the colder body, the entropy of the system and surroundings shall increase. This change in overall entropy accounts for the irreversibility of the process under examination.
Exergy
It amounts to the maximum useful work performed by the system.
This concept is slightly different from that of energy, which is the measure of the total energy contained by any system, say, in the form of heat. In contrast, exergy is the useful or purposive potential of that energy.
In general, it is the energy differential (or the energy difference) between two energy states: one when the body is in its initial state and the other when it is assumed to be in its stable state, say when it is in thermal equilibrium with its surroundings.
Energy loss is also a key term used in literature. It refers to the loss of energy during the energy conversion process, for instance, in the conversion of high-temperature steam into that of lower one. The heat lost to the surroundings during the process is thus of no use and is called anergy.
Exergy in European textbooks is also called essergy (the essence of energy). Its other names are utilizable energy or availability.
Enthalpy
It refers to the total energy content of the system.
Theoretically speaking, it amounts to the sum of the internal energy of the system and the product of pressure and volume.
Enthalpy change refers to the change that a system encounters during heat transfer processes. But why? Because, in the heat transfer processes, the internal energy of the system changes.
Hence, enthalpy change can be either positive or negative. It is positive during the endothermic processes during which the system absorbs heat, whereas, in exothermic ones, the enthalpy change is negative because the system loses heat.
It is a pure thermodynamic term that is frequently concerned with the energy analysis of a system subject to heat transfer.
There are different types of enthalpy, such as enthalpy of combustion, enthalpy of formation, enthalpy of vaporization, and so on.
The importance of enthalpy is invested in the analysis of steam turbines and steam properties represented in the tabular or graphical form.
Point Function and State Function
The properties of any thermodynamic system are represented by two key concepts: point function and path function.
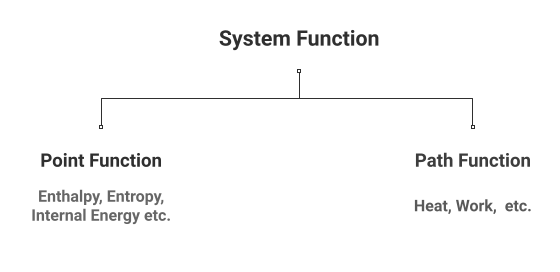
Point Function
It is the property of a system that is determined by its present state or a state at a specific point in time, regardless of the path adopted to bring that state. Its examples include enthalpy, entropy, and internal energy, among many others.
But how is the value of the point function actually determined? It is determined by using the state variables of the system, such as its temperature, pressure, and volume at a specific point in time where the value of state function (say enthalpy, entropy, and internal energy) is to be calculated.
For example, during the (say adiabatic) expansion of an ideal gas from initial state A to final state B, its volume at final state B would be the arithmetic difference of two volumes.
These properties are also called the thermodynamic coordinates of the system. Together, they define the state as thermodynamic state space, which is also called equilibrium state space or simply state space.
Path Function
It is wrong to say that it is the property of a system as such. Rather, it refers to the change in the thermodynamic behavior of a system, which depends on the means through which such change is made possible.
Its examples include heat and work.
In simple words, if an ideal gas is passed from initial state A to final state B, then net heat transfer depends on the path, which means whether such a transfer of heat is isothermally or adiabatically carried out. In both cases, the value of heat transfer at state B might be the same, but the net heat exchange would be different as it is path-dependent.
One can say that it cannot be simply the arithmetic difference of two heats, as is the case with the point function.
I am the author of Mechanical Mentor. Graduated in mechanical engineering from University of Engineering and Technology (UET), I currently hold a senior position in one of the largest manufacturers of home appliances in the country: Pak Elektron Limited (PEL).
